Проектирование кристаллов.

Выходные данные учебного пособия – Основные разделы кристаллографии: учебное пособие / Кузьмичева Г.М. – М.: МИТХТ, 2002. – 80 с.

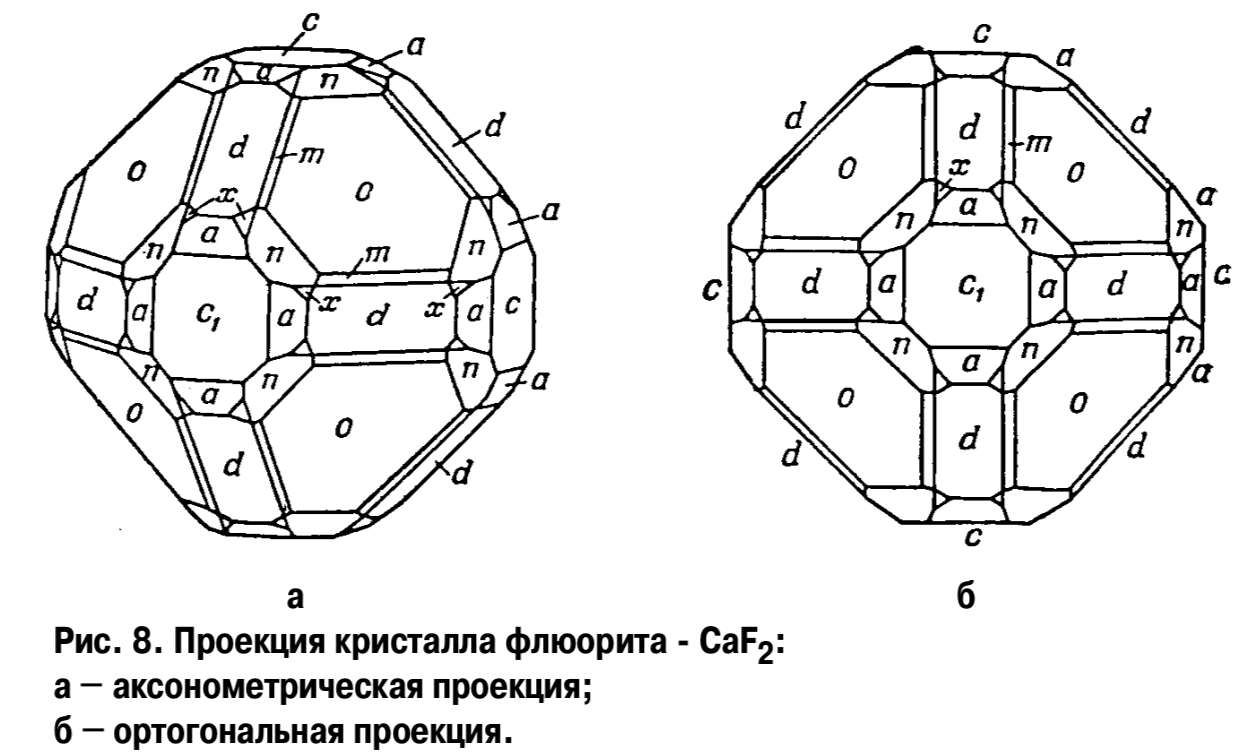
В кристаллографии для этого пользуются обычно двумя методами:образным, или перспективным (ортогональные и аксонометрические проекции) (рис. 8) и графическим (графические проекции). В последнем случае кристалл может проектироваться на поверхность сферы (сферическая проекция), экваториальную плоскость сферы (стереографическая и гномостереографическая проекции) и плоскость, касательную к северному (верхнему) полюсу сферы (гномоническая проекция).

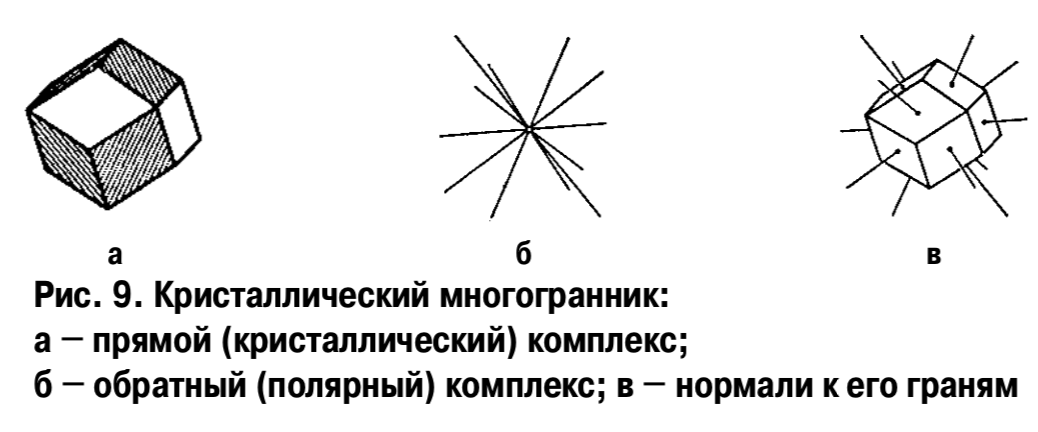
Образное проектирование не выявляет в достаточной степени действительные величины углов между гранями, что позволяют сделать графические проекции. При этом кристалл может быть представлен или в виде прямого (кристаллического) комплекса (рис.9а), или в виде обратного (полярного) комплекса (рис. 9б). В последнем случае каждая грань кристалла заменяется на нормаль к ней, которая и проектируется (рис. 9в).

Сферическая проекция

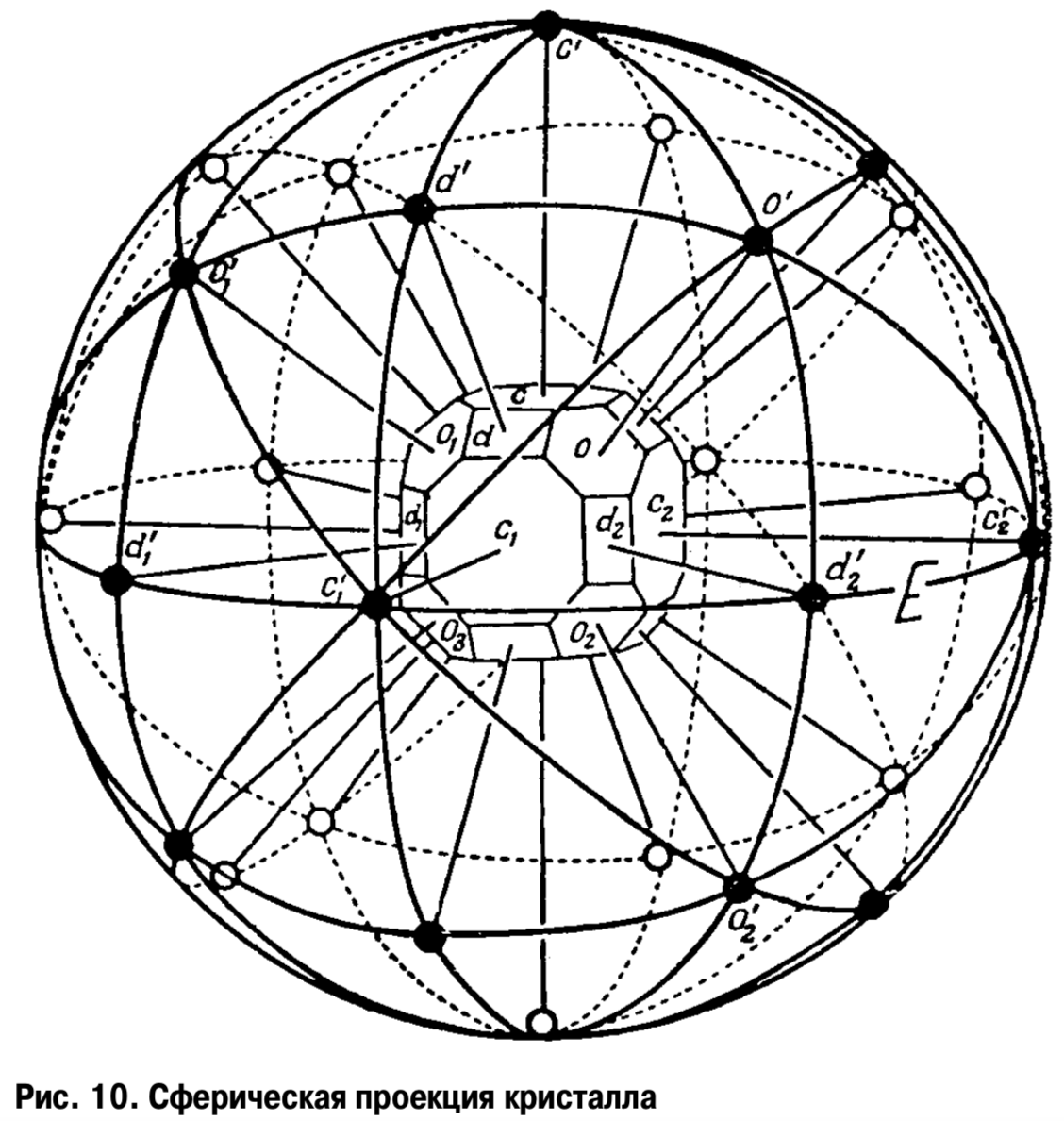
Из точки пересечения прямых, перпендикулярных граням, опишем сферу. Пересечение нормалей к граням кристалла с поверхностью сферы представляет собой сферическую проекцию нормалей к граням кристалла. Каждая нормаль проектируется на поверхность сферы проекций в виде точки. Каждой из точек проекции отвечает одна из граней кристалла (рис. 10).
Сферическую проекцию кристалла можно строить без замены грани кристалла их нормалями. В этом случае все грани кристалла путем параллельного переноса перемещают в центр сферы проекций и строят следы пересечения этих граней со сферой проекций (рис. 10).

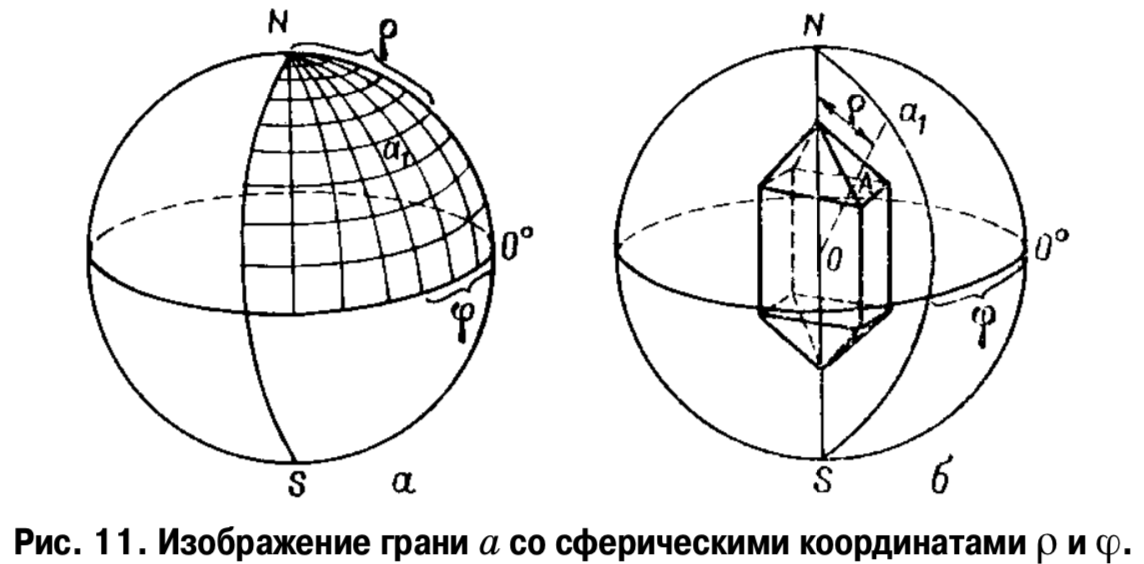
Положение любой точки на поверхности сферы можно охарактеризовать двумя сферическими координатами ρ (долгота) и φ (широта) (рис. 11).
Сферическая проекция кристалла наглядна, но для практического применения ее удобнее спроектировать на плоскость. Для этого пользуются стереографическими, гномостереографическими и гномоническими проекциями. 

Стереографическая проекция

За плоскость стереографической проекции выбирается экваториальная плоскость P, на которую сфера проектируется в виде круга проекций (рис. 12).


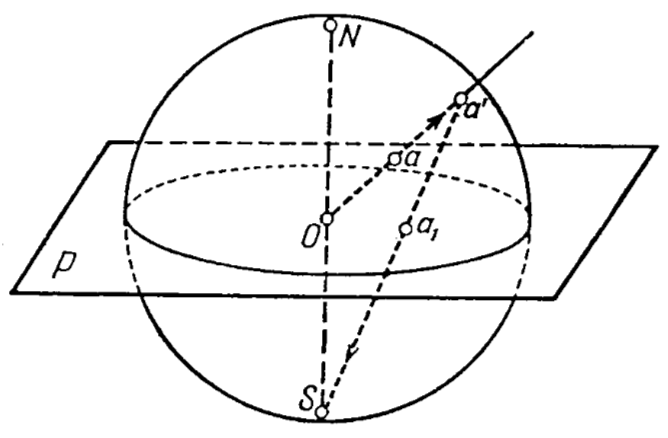
Рис. 12. Стереографическая проекция точки

Чтобы спроектировать точку a, находящуюся внутри сферы с определенным радиусом, на поверхность сферы, проводим из центра O через точку a прямую до пересечения со сферой; полученная при этом точка a' сферическая проекция точки a. Соединяя точку a' с южным (нижним) полюсом S, получим на плоскости P точку a1 - стереографическую проекцию точки a (рис. 12).
При проектировании прямой линии (направления) AB (рис. 13), проходящую через центр сферы и пересекающую ее поверхность в точках m и n, сначала находят проекции m' и n' этих точек на экваториальную плоскость Р, используя южный (нижний) и северный (верхний) полюсы сферы соответственно. Затем соединяют точки m' и n' и получают проекцию прямой mn. Так как прямая AB проходит через верхнюю (BO) и нижнюю (OA) половины сферы, отрезок ее проекции m'O изображается сплошной линией, а On' – пунктирной. Точка O является общей точкой для стереографической проекции и для проектируемой прямой и расположена в экваториальной плоскости (рис. 13).

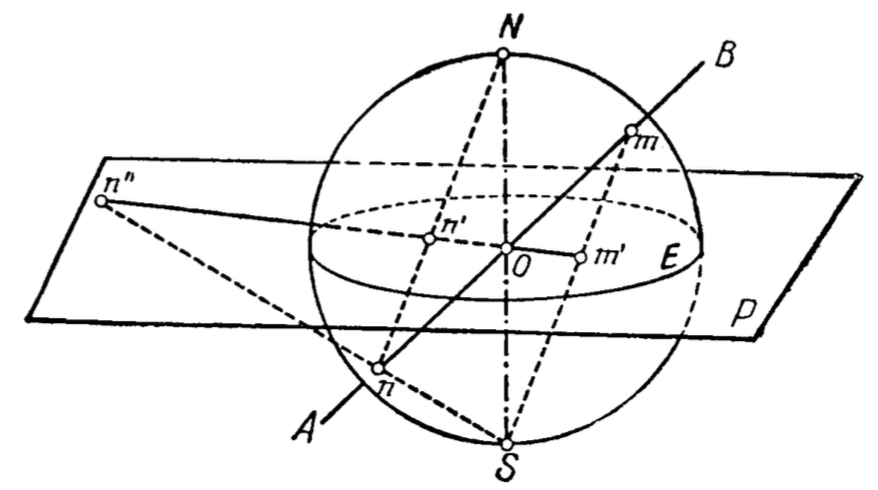
Рис. 13. Стереографическое изображение прямой

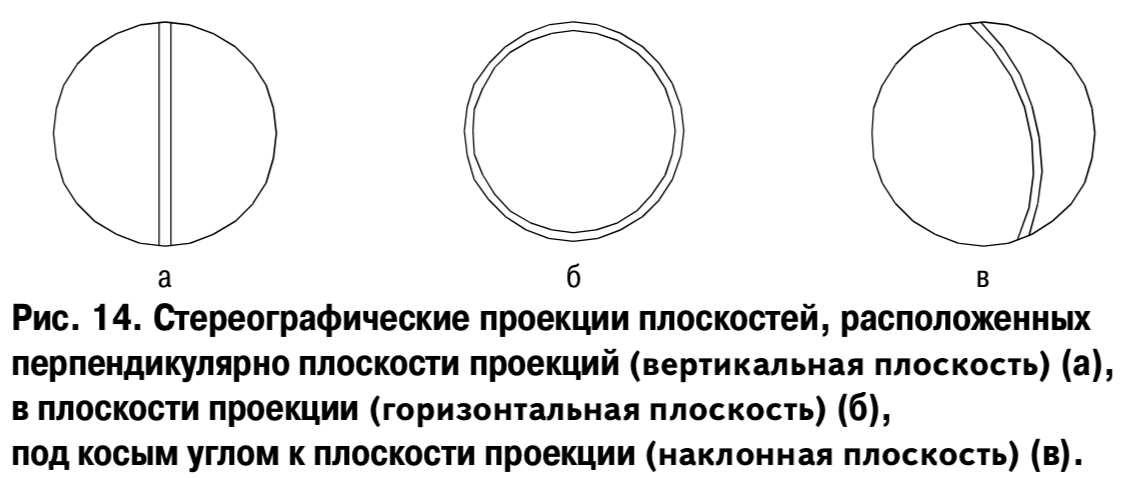
Стереографические проекция изображаются внутри круга (рис. 14).

Свойства стереографической проекции

1.Любая окружность, проведенная на сфере, изображается на стереографической проекции также окружностью (в частном случае прямой линией).
2.На стереографической проекции не искажаются угловые соотношения: угол между нормалями к граням (полюсами граней) на сфере (измеренный по дугам больших кругов) равен углу между стереографическими проекциями тех же дуг.
3.При повороте сферы вокруг диаметра, проходящего через полюс, на плоскости происходит поворот вокруг точки ее касания со сферой на тот же угол. Стереографические проекции применяются главным образом для изображения элементов симметрии кристаллов (рис. 15).

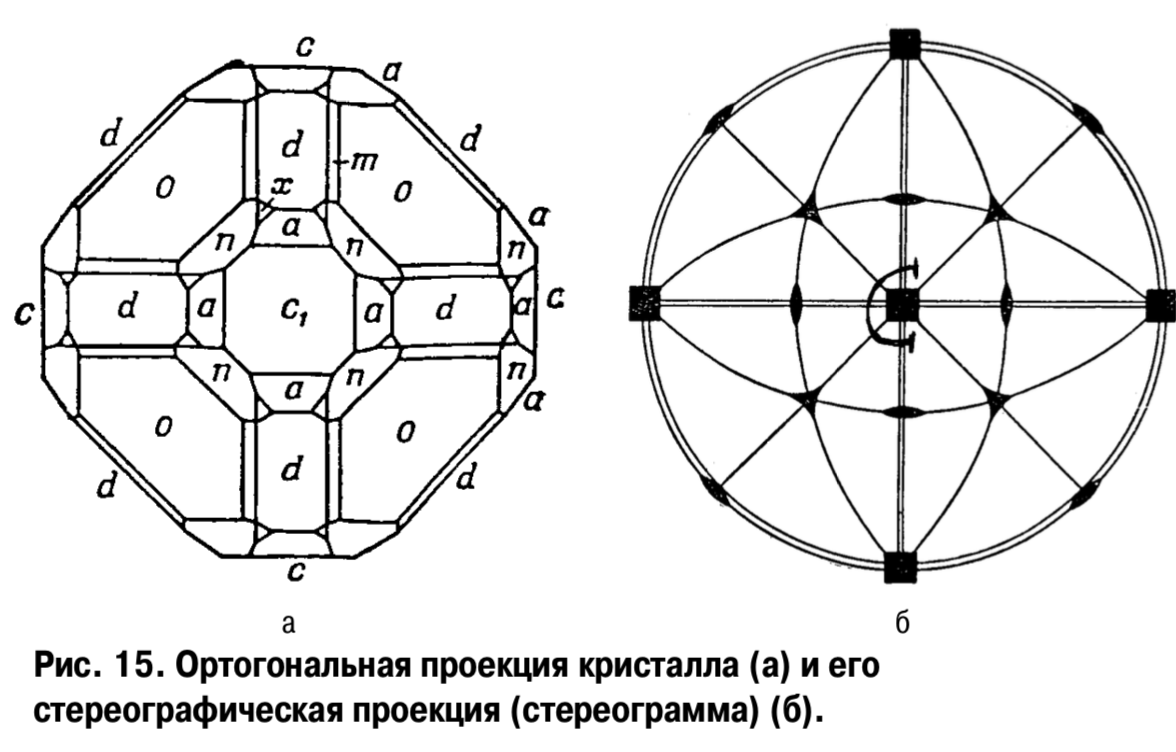
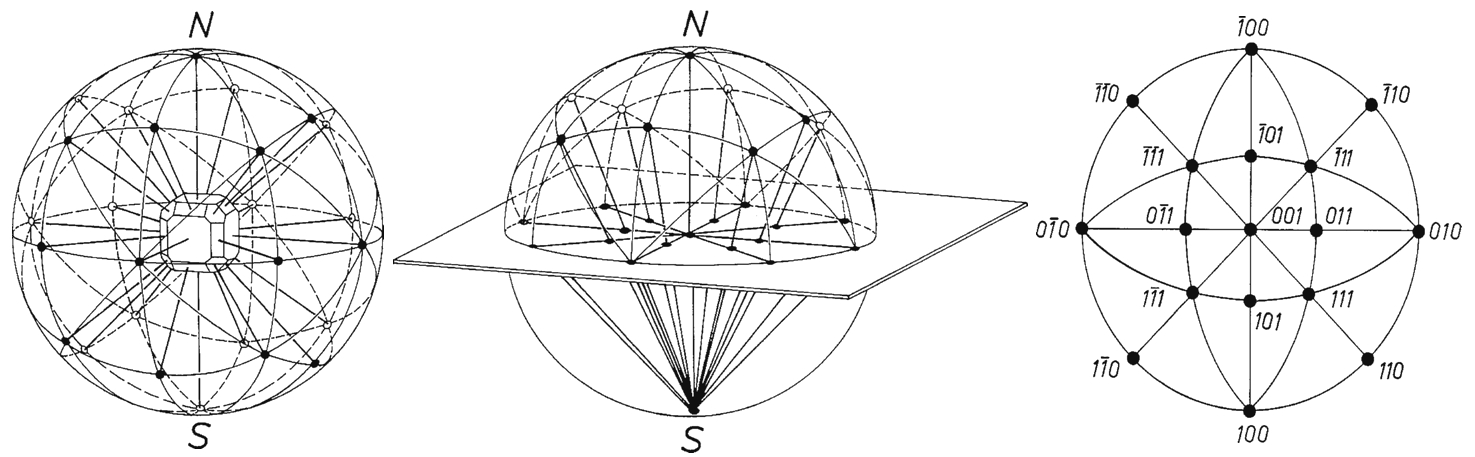
Рис. Построение стереографической проекции кристалла

Гномостереографическая проекция

Этот вид проекции чаще всего применяется для изображения кристаллических многогранников. При этом проектируется не многогранник, а его полярный комплекс, т.е. не грань кристалла, а нормаль к грани. Плоскостью гномостереографической проекции служит та же экваториальная плоскость сферы проекций Р, как и для стереографической проекции. Гномостереографическая проекция кристалла представляет собой совокупность стереографических проекций нормалей к граням кристалла (рис. 16).

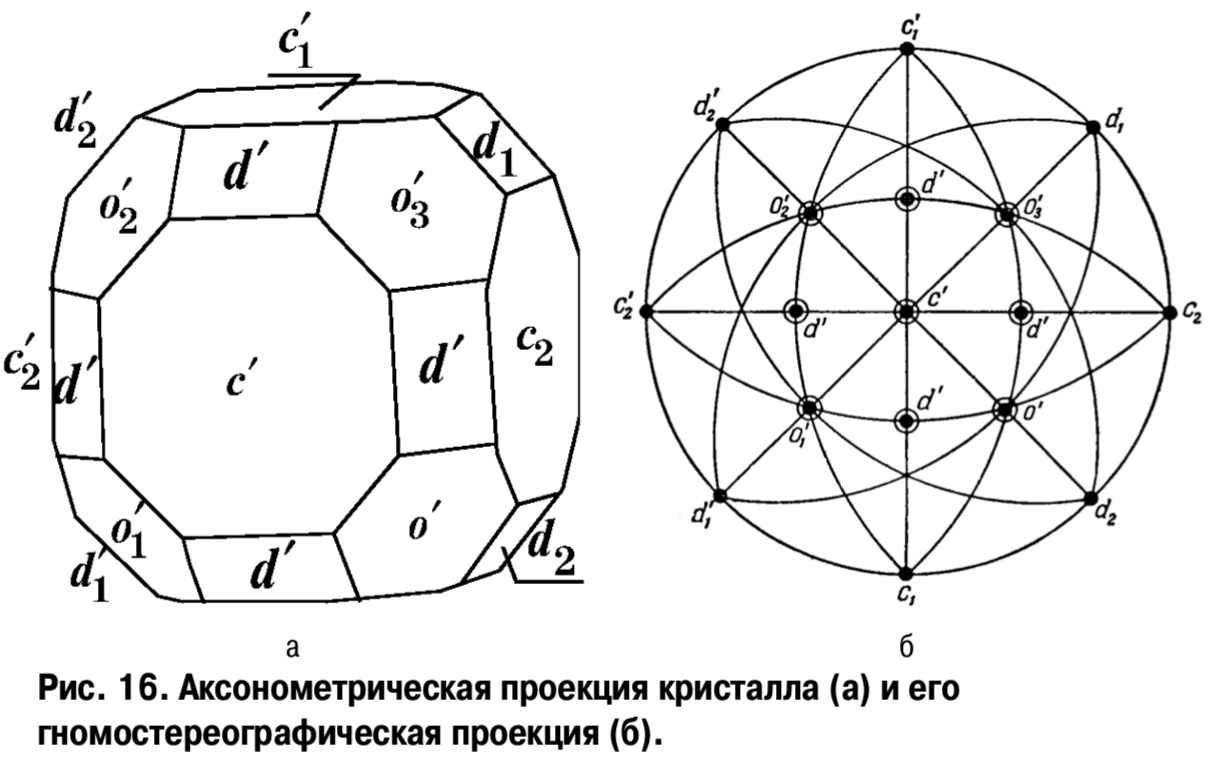
Свойства гномостереографической проекции

1. Горизонтальные грани проектируются в центре круга проекции. 2. Вертикальные грани проектируются на основном круге проекции; 3. Наклонные грани проектируются внутри основного круга, причем чем круче наклон, тем дальше от центра располагается проектирующая ее точка.

Гномическая проекция

Плоскость гномонической проекции параллельна плоскости стереографической и гномостереографической проекций, но она не экваториальная, а касательная к северному полюсу сферы проекции. Нормаль к грани кристалла, проведенная из центра сферы проекций, продолжается до пересечения с плоскостью проекции. Плоскости граней, перпендикулярных плоскости проекции, отодвигаются в бесконечность. Их положение указывается стрелкой (рис. 17).

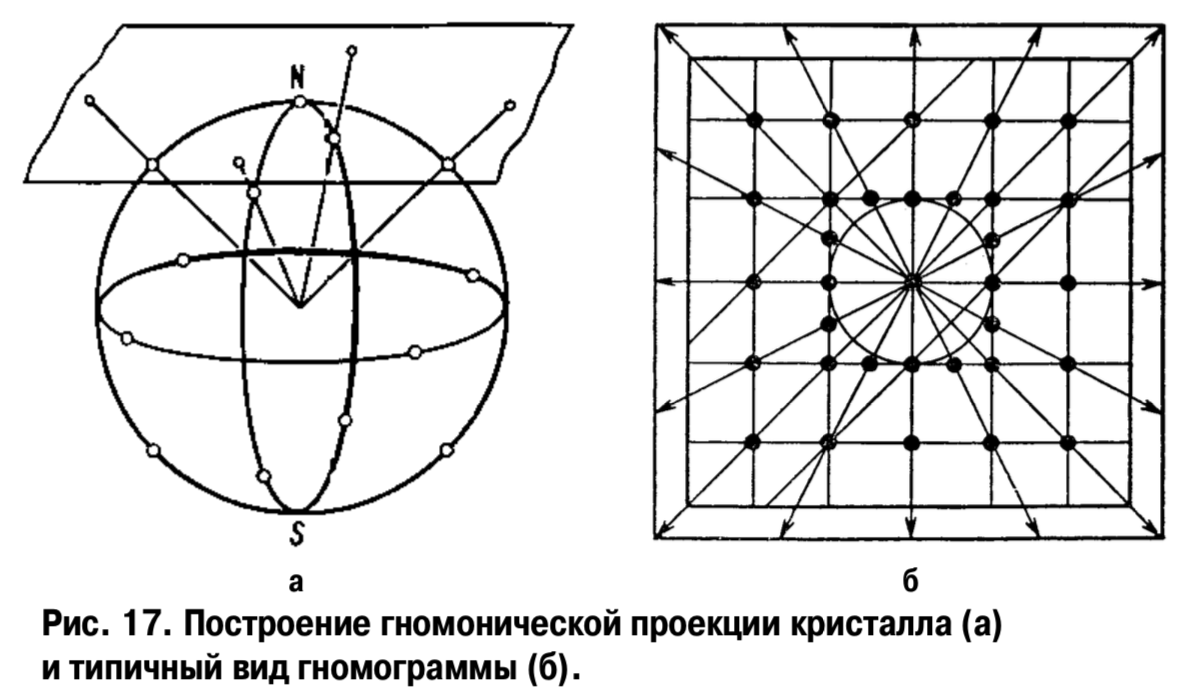
Гномоническая проекция плоскости представляет собой точку, проекция направления – прямую. Проекции граней одной зоны лежат на одной прямой. Зона – совокупность граней, параллельных одному ребру, так называемой оси зоны, т.е. зону образует комплекс граней, нормали к которым лежат в одной плоскости.
Недостатком гномонической проекции является то, что в ней не сохранены угловые соотношения: углы между линиями зон на проекции не равны углам между соответствующими плоскостями одной зоны.
Этот вид проекции широко применяется в дифракционных методах исследования.

Соотношения между сферической, стереографической, гномостереографической и гномонической проекциями

Принцип построения стереографической и гномостереографической проекций одинаков, различие заключается в том, что стереографическая проекция строится по прямому (кристаллическому) комплексу граней кристалла, а гномостереографическая проекция – по обратному (полярному) комплексу. Иногда их совмещают на одном чертеже, изображая элементы симметрии кристалла с помощью стереографической проекции, а грани и ребра – с помощью гномостереографической.
На гномостереографической проекции (плоскость проектирования P) точка a1 – это проекция плоскости (грани), перпендикулярной Oa, так как в этом виде проектирования грань заменяются нормалью к грани (Oa – нормаль к грани). С другой стороны, Oa′ – это стереографическая проекция направления Oa. На гномонической проекции (плоскость проектирования М) точка a2 – гномоническая проекция той же плоскости, нормаль к которой Oa. (рис. 18).